提示: 想要体验更新更强大的 ChatGPT 需要升级到 Plus会员, 详情请参考 ChatGPT Plus升级教程
近年来，AI技术的发展已经从基础任务处理逐渐向更复杂的推理场景迈进。Kimi近日发布的两项创新成果：数学推理模型 k0-math 和强化搜索版本 Kimi 探索版，为这一趋势带来全新可能。
k0-math：AI数学推理的新高峰
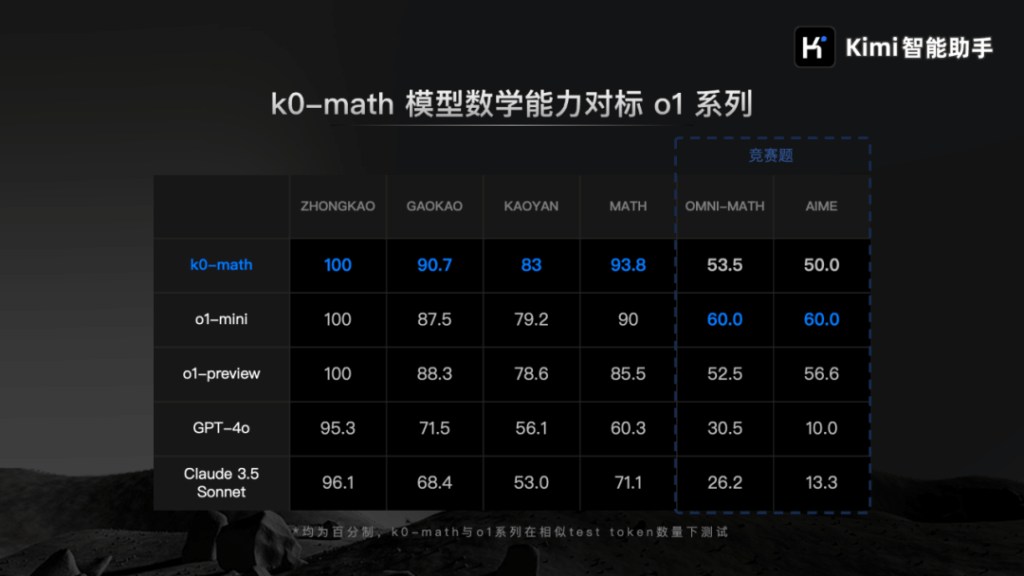
作为 Kimi 的首款强化推理模型，k0-math 融合了强化学习与思维链技术，能够模拟人脑的反思和规划过程，在数学问题求解上取得显著突破。k0-math 的性能在中考、高考、考研及竞赛级测试（如 MATH 和 AIME）中表现优异，甚至在多个基准测试上超越 OpenAI 的 o1-mini 和 o1-preview 模型。尤其是在 MATH 测试中，其得分达到 93.8，仅次于尚未公开的 o1 完全版。
不仅如此，k0-math 在复杂数学题目上的表现令人印象深刻。它能够通过探索和试错，不断调整解题策略，最终得出正确答案。然而，当前版本也存在一定局限性，例如对于几何类问题的适配不足，以及对极其简单问题的过度推理。这些问题将在后续迭代中逐步优化。
Kimi 探索版：从搜索到推理的智能跃升
Kimi 探索版专注于 AI 搜索的强化学习应用，通过意图增强、信源分析和链式思考三大能力，显著提升搜索效率与精准性。与传统搜索引擎不同，Kimi 探索版能够从模糊或抽象问题中提炼核心意图。例如，当用户调研“用户忠诚度”时，AI 会主动转化为具体的关键指标（如留存率、活跃度），并进行深度检索。
此外，Kimi 探索版具备强大的信源筛选能力，能够从海量搜索结果中提取最权威、最新的内容，并提供精确的溯源链接。这一特性尤其受到科研人员和咨询顾问的青睐。同时，其链式思考能力可以高效分解复杂问题，例如程序员在技术选型时，Kimi 能从多个维度给出基于具体场景的推荐。
AI推理的边界扩展
Kimi 的最新进展标志着 AI 技术从工具型助手向智力伙伴的转型。这些创新不仅将在数学和搜索场景中带来直接收益，还预示了在科学研究和复杂工程领域的广泛应用可能。未来，k0-math 和 Kimi 探索版将逐步上线，帮助用户迎接更具挑战性的任务，解锁 AI 潜力的全新边界。
关注公众号 AI小路灯
回复 [ 资料 ] 即可获取ChatGPT变现课程
回复 [ 巨头 ] 即可获取国内"AI巨头"直播课
文章评论